5963: Problem c

经过调查，小Z意识到全国范围内已有大量的潜在的病毒携带者，如果爆发，后果将不堪设想。因此需要立即对这种病毒进行研究。 
经过初步观察，小Z的团队发现了一种奇怪的现象：我们将显微镜下的图片看做是一个二维的平面，每个病毒都有一个坐标（x,y）。他们发现，对于某一个病毒，总能找到另一个病毒（可以是自己）关于同一个坐标中心对称。这个中心对称点，是所有病毒共同拥有的。 
所谓中心对称，就是说有两个坐标(x1,y1)和(x2,y2),那么((x1+x2)/2,(y1+y2)/2)就是这对点的对称中心，也可以说这对点关于((x1+x2)/2,(y1+y2)/2)中心对称。特别地，(x,y）可以关于自身中心对称。 
现在你知道了n个病毒的坐标，请帮助小Z的团队找到这n个病毒共同的对称中心。 

第一行一个整数n，表示病毒的数目。 
接下来n行，每行两个整数x,y，用空格隔开，表示病毒的坐标(x,y)。 

 一行两个整数，用空格隔开，分表表示对称中心的x坐标和y坐标。我们保证存在这样的坐标，并且都是整数且唯一。

【样例1输入】
2
1 1
3 3
【样例2输入】
6
1 3
4 2
6 2
7 5
4 6
2 6

【样例1输出】
2 2
【样例2输出】
4 4

【样例1解释】

(2,2)是(1,1)和(3,3)的对称中心，因为(1+3)/2=2。

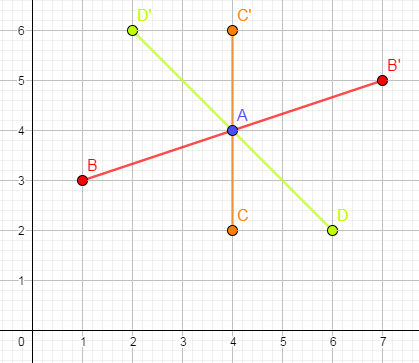
【样例2解释】

如图所示：

【数据范围】

对于20%的数据，n=2。

对于另外30%的数据，y=0，即坐标都在x轴上。

对于另外30%的数据，n<=100。

对于前面这80%的数据，n是偶数，所有坐标都在[-50,50]之间。

对于100%的数据，n<=100000，保证有解，x和y的和不超过1,000,000,000。可能有负数。数据有梯度。