6197: 吃豆人

有一个 n 行 n 列的正方形点阵，左上角点坐标为 $(1,1)$，右下角点坐标为 (n, n)。

点阵中每个整点上都有数量不一的豆子，坐标为 (i, j) 的点上有ai,j 个豆子。

你可以放置吃豆人，可以将点阵中任意的整点作为吃豆人的初始位置，再给定左上、左下、右上、右下之一作为吃豆人的初始方向。

吃豆人会不断沿初始方向行进，吃光遇到的所有豆子，直到碰到点阵的边界，此时：

1. 如果吃豆人处于正方形点阵四个角之一的位置，那么就会停止行动；
   
2. 否则，吃豆人的行进路线将以这条边界为镜面发生反射，下图展示了一个路径某两次发生反射的例子：
   

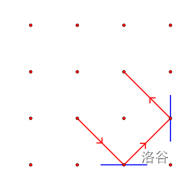
现在，你需要放置两个吃豆人，求两个吃豆人最多共能吃到多少个豆子？注意同一个豆子只能被吃一次。

第一行包含一个整数 n，表示点阵大小。

接下来 n行，每行包含 n个整数，其中第 i行第 j个整数表示 ai,j。

4
20 1 19 2
3 18 4 17
16 5 15 6
7 14 8 13

132

在 $(1,1)$ 和 $(1,3)$ 位置放置吃豆人，初始方向分别为右下和左下，即可吃到位于 $(1,1)$，$(1,3)$，$(2,2)$，$(2,4)$，$(3,1)$，$(3,3)$，$4,2)$，$(4,4)$ 位置上的豆子，总个数为 $132$， 达到最大，路径分别如下图绿线和红线所示：

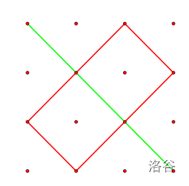
对于 $30\%$ 的数据，$n\le 3$。

对于 $60\%$ 的数据：$n\le 100$。

对于 $100\%$ 的数据：$2\le n\le 1000$， 10000≤ai,j≤1000。