Description
小Y有一个 n*n棋盘,开始时这个棋盘每个格子的颜色是白黑相间的,即第一行的第1,3,5……个格子是白色,第2,4,6……个格子是黑色,第二行第2,4,6……个格子是白色,第1,3,5……个格子是黑色,如下图所示。

小Y会进行q次操作,每次操作会将某一行或者某一列的所有格子的颜色反转,即白色格子变成黑色格子,黑色格子变成白色格子。小Y想知道,在每次操作之后,一共有多少个同颜色(全黑或全白)的联通区域。这里联通指的是四联通,即两个格子之间有边相邻才算联通。
Input
第一行2个正整数n,q,表示棋盘的大小和操作的次数。
第2到q+1行每行2个正整数opt[i],a[i],若opt[i]为1则表示反转的是行,为2则表示反转的是列,a[i]表示反转的是第几行/列。
Output
输出q行每行一个整数,表示在经过该次操作后,一共有多少个同颜色的联通区域。
Sample Input Copy
样例输入1
3 3
1 2
2 3
1 2
样例输入2
100000 1
1 1
样例输入3
15000 5
1 90
1 1231
1 91
1 1233
1 1232
Sample Output Copy
样例输出1
3
2
6
样例输出2
9999900000
样例输出3
224970000
224940000
224940000
224910000
224940000
HINT
样例解释1
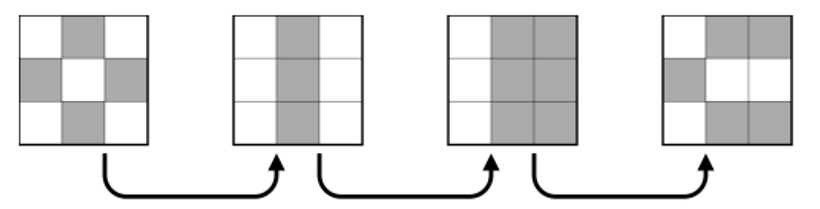
初始棋盘白黑相间,第一次操作后有3个同颜色的联通区域,第二次操作后有2个同颜色的联通区域,第三次操作后有6个同颜色的联通区域。
数据范围
本题共有10个测试点,每个测试点12分
对于全部测试点:1≤q, n≤10^5,
1≤opt[i]≤2, 1≤a[i]≤n
对于测试点1-4:1≤n≤4, 1≤q≤10
对于测试点5-6:1≤n≤10^5, q=1
对于测试点7-9:1≤n≤10^5, 保证同一个测试点所有的opt[i]均相等